素数计算 - Sieve of Eratosthenes

Eratosthenes筛选法的思路

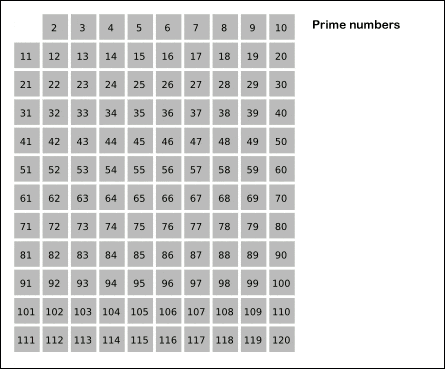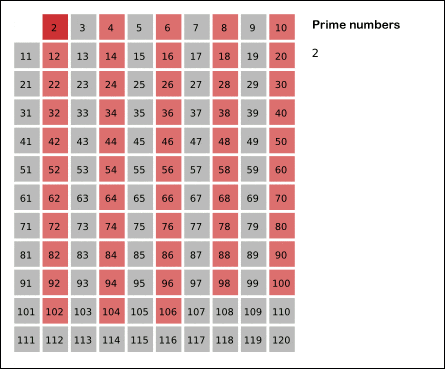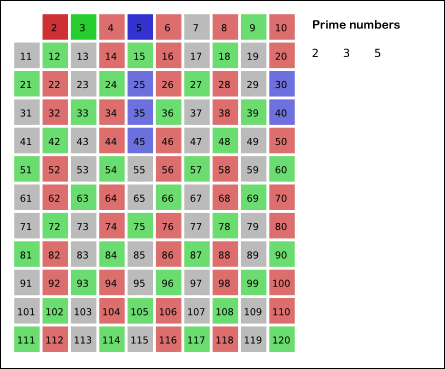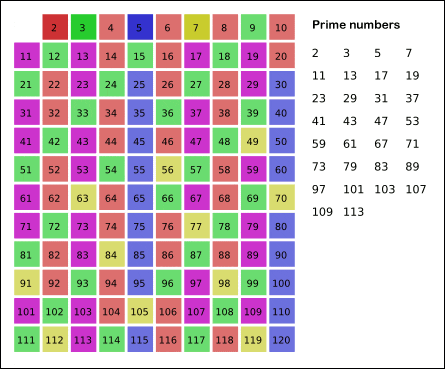
找到素数是很麻烦的一件事情，但是做排除一个合数是很简单的。首先从 2 开始，我们知道 2 是一个素数，那么 2的倍数就都不可能是素数了。然后我们发现 3 也是素数，那么同理排除掉所有3的倍数。由此不断排除后，剩下的就是素数了。

Sieve of Eratosthenes的一些优化细节

• 由于因子的对称性，我们筛选操作只需要遍历[2,sqrt(n)]就够了。
• 筛选操作会包含一些重复计算，比如i = 5时算法会标记 10，15 等数字
  但是这两个数字已经被i = 2和i = 3的 2 × 5 和 3 × 5 标记了。
  所以我们可以稍微优化一下，直接从i的平方开始合数标记。

---

• 我们已经知道了所有的偶数都不会是素数，那么就不需要再花费算力来将整整一半的数据标记为合数了。可以直接从3开始遍历[3,sqrt(n)] ,设定for循环的步长为2，跳过所有偶数。
  同时，在筛选操作的时候也要避免偶数，这一点具体看代码

代码示例

public int countPrimes(int n) {
    if (n <= 2) return 0;
    int ans = 1;// don't forget to record 2. :-)
    boolean[] isCompositeArr = new boolean[n]; 
    int upper = (int) Math.sqrt(n);
    for (int i = 3; i < n; i = i + 2) { //1.scan only odd number
        if (isCompositeArr[i]) continue;
        ans++;
        if (i > upper) continue; //2. avoid i^2 overflow.
        for (int j = i * i; j < n; j = j + 2 * i) {//j初始化为 i^2来避免重复计算，同事j每次增加2i,来跳过偶数，保持j只标记奇数。
            isCompositeArr[j] = true;
        }
    }
    return ans;
}