LeetCode - 前缀和技巧
求区间元素和
L303 区域和检索 - 数组不可变
为了计算一个区间内所有元素的和,我们可以为每个元素维护一个前缀和,表示从开头到该元素的所有元素的和。这样,通过计算区间终点的前缀和减去起点前缀和,可以得到该区间内元素的和。这种方法可以有效地减少重复计算,提高计算效率。
求二维区间的元素和
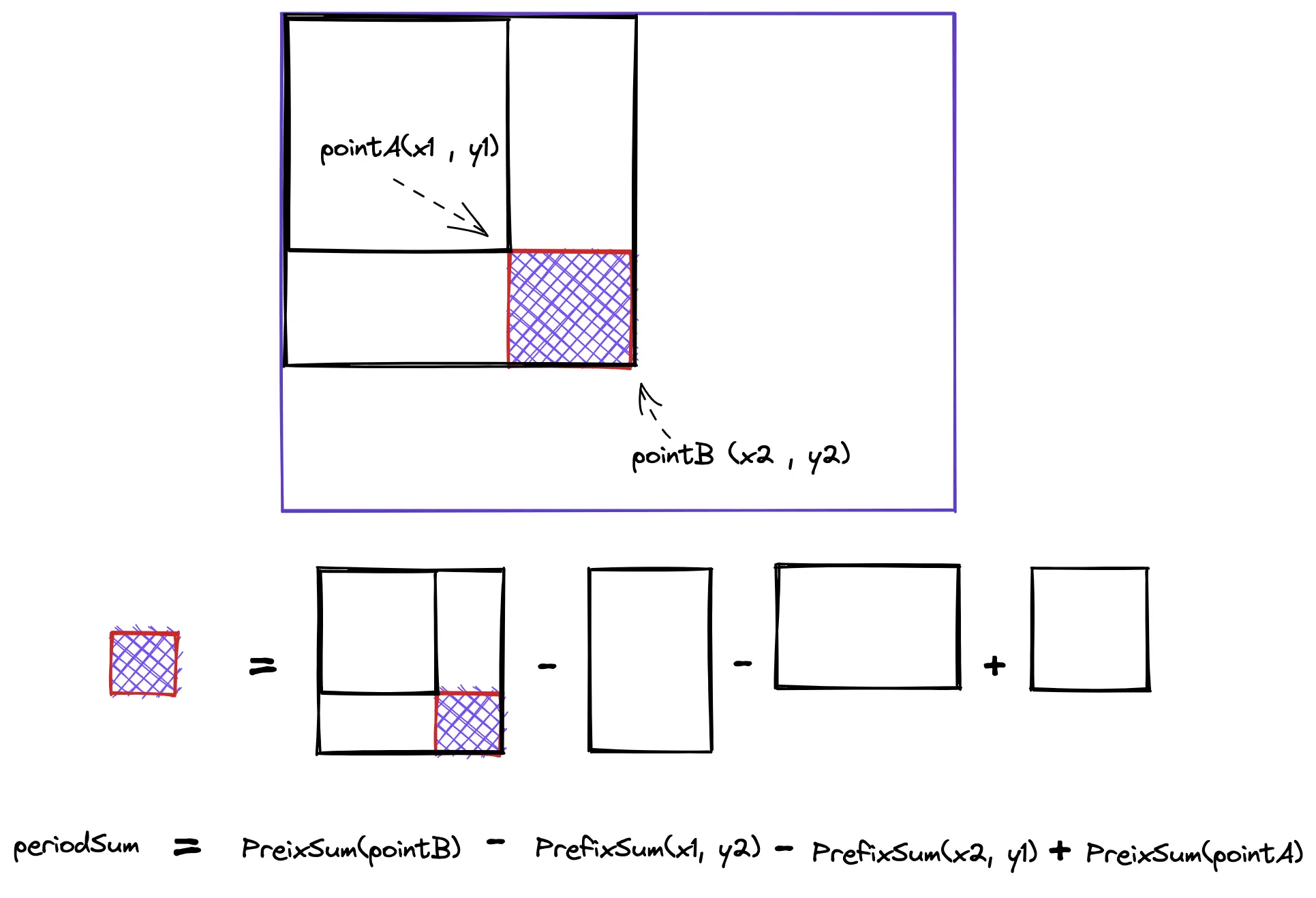
L304 二维区域和检索 - 矩阵不可变
当区间变为二维时,我们仍然可以沿用前缀和的思路进行求解。但是不能直接用终点减去起点前缀和,而是需要采用一些新的技巧。
L1314 矩阵区域和
将题目从数学术语转化为日常语言:给定一个宽度 k,将原矩阵划分成大小为 k 的子矩阵,每个子矩阵的和作为新矩阵中对应位置的元素。重用L304的代码后就能很快做出。
前缀后缀一起用,求除当前元素外的所有元素和/积
L724 寻找数组的中心下标
中心下标是数组的一个索引,其左侧所有元素相加的和等于右侧所有元素相加的和。
解法是维护前缀和与后缀和即可 leftSum = prefixSum[i-1] rightSum = suffixSum[i+1]
虽然习惯于起始位置来初始化前缀和,但这并不是固定的,像这道题中就是从终点开始初始化后缀和,两者共同使用完成任务。
L238 除自身以外数组的乘积
前缀和数组中的两个元素之差是子数组元素之和,那么如果构造「前缀积」数组,那么两个元素相除就是子数组元素之积。所以我们构造一个 prefix 数组记录「前缀积」,再用一个 suffix 记录「后缀积」,根据前缀和后缀积就能计算除了当前元素之外其他元素的积。
sumOfLeftProduct = prefixProduct[i-1]
sumOfRightProduct = suffixProduct[i+1]
reslt = sumOfLeftProduc * sumOfRightProduc
求特定区间 - 配合Map
有些题目的解法中的前缀和可以直接用一个currentSum/status变量替代,因为我们操作的都是当下时刻的前缀和,且很快就存到了Map中,我们没有获取特定时刻的preSum的需求,而是往往需要根据preSum找到其对应的index。
L530 和为 K 的子数组的个数
在 nums 中寻找和为 K 的子数组的个数
做法是维护一个presum的CountMap,在计算完currentPresum时,动态地在map中查找target - currentPresums 是否在CountMap中,是则获取其count加到res中。
就像tips中提到的那样,这道题的解法中其实不需要显式保存一个preSum数组,因为我们操作的一直都是CurrentSum
L325 和为 k 的最长子数组长度
和上一题一样,做个小改动就行。
上一题是维护一个sumToCount的map,在循环体中不断更新count个数,并把currentSum更新到CountMap中
本题是维护一个sumToIndex的map,在循环体中不断更新最长的长度,并且不覆写map中的数据,因为我们要尽可能大的length,(如果求minLength,则需要更新map中的index)
求特定区间变体 - 前缀和表示status
L525 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
这里可以维护一个前缀和,将0视作-1,然后题目就转换成了求区间和为0的最长子数组。而这一问题的解法就在上一节。
同样的,就像前面的tips里提到的那样,可以用一个status变量来优化presum。问题变成了找到status相同的indexB,求indexA ~ indexB的最大长度
L1124 表现良好的最长时间段
上面一题的复杂变体,status改变与否的阈值是8: status = hours[i] > 8 ? status + 1 : status - 1;而需要得到的是区间要求是beginStatus < endStatus。
一种做法是status初始化为0,然后若当前status>0,那么此时的 0~currentIndex就是一个有效区间
接着若当前status不为正数,那么找到status - 1 在index的map中是否存在,测试的IndexinMap ~ currentIndex 就是一个有效区间。
求特定区间变体 - 前缀和公式代换
有些题目将问题翻译成数学公式后,可能会让我们更容易看出其中的规律和规则,这为我们提供了一些洞见。本节中的题目就是这种类型
L523 连续的子数组和 满足区间和为k的倍数
给你一个整数数组 nums 和一个整数 k,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:子数组大小 至少为 2,且子数组元素总和为 k 的倍数。如果存在,返回 true;否则,返回 false
翻译一下就是寻找 i, j 使得 $(preSum[i] - preSum[j]) \mod k = 0$ 且 $i - j \geq 2$。另外该等式 其实就是 $preSum[i] \mod k = preSum[j] \mod k$。那么最终使用一个哈希表,记录 preSum[j] % k 的值以及对应的索引,就可以迅速判断 preSum[i] 是否符合条件了。
L974 和可被 K 整除的子数组
类似的,这道题目和上面一题是完全一样的,只是上面一题只需要判断有无,这题要求出个数
解题的关键还是将题目翻译为$(preSum[i] - preSum[j]) \mod k = 0$ 并转换为$preSum[i] \mod k = preSum[j] \mod k$ 等式