LeetCode - 更多双指针的技巧

链表删重

L82 删除排序链表中的重复元素 II

distinct的加强操作，不是去重，而是只要重复就全部删除。

思路上的双指针就是一个用于遍历元素，一个用于组成新的链表

medium的难点是处理linkedlist的节点问题，在循环遍历的循环体中进行条件判断的代码编写需要一点技巧,在内部维护boolean表示当前遍历的是否为重复元素的写法比较好。

while (p != null) {
  boolean isDup = false;
  while (p.next != null && p.next.val == p.val) {
    isDup = true;
    p = p.next; //此时p指向重复元素中的最后一个
  }
  if (!isDup) {
    result.next = p;
    result = result.next;
  }
  p = p.next;//再次移动以跳过所有重复节点
}

这道题除了指针，还可用递归。

L1836 从未排序的链表中移除重复元素 （付费）

和82一样，删除所有重复元素，但是此处list是未排序的。

思路上是先遍历一遍，Hashmap valTOCount统计每个元素出现的次数，然后第二次遍历，对每一个元素查map，出现次数大于1就跳过，然后对不重复的元素进行拼接。

代码上其实比82简单了，拼接与否的判定就是查map，很直接。

多路并归

L264 丑数 II

其实这类算是一种套路题，知者不难，难者不会，所有的丑数的做题思路单独做一个笔记……这里不单独赘述

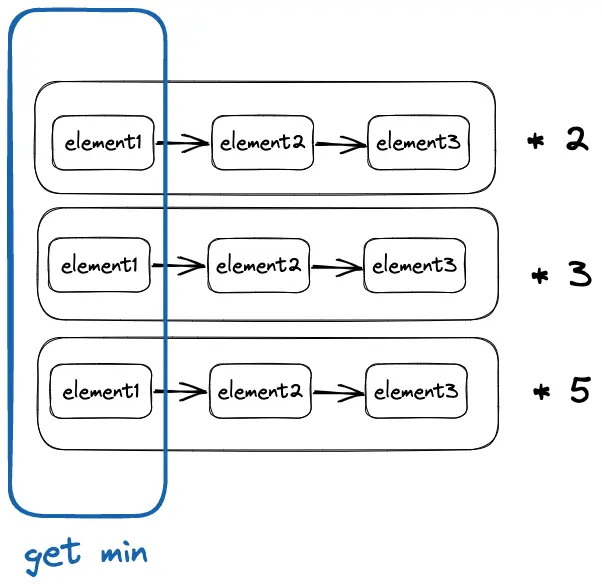
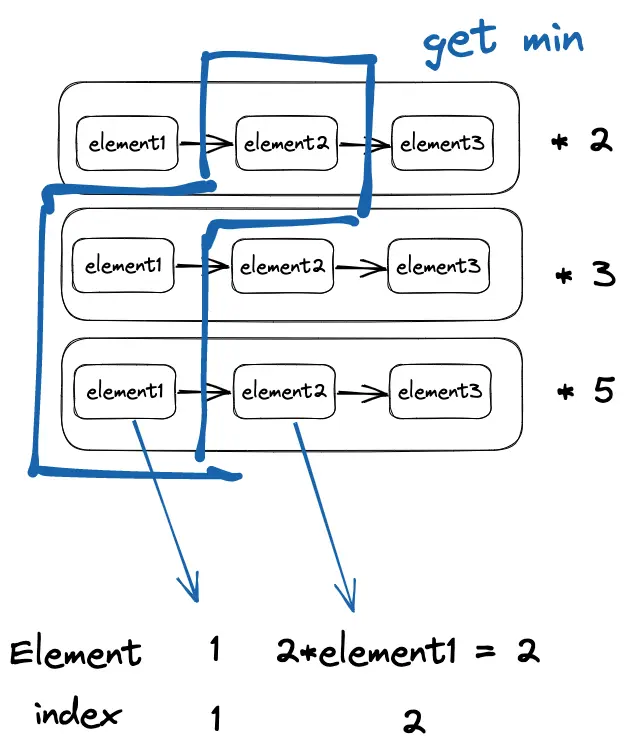
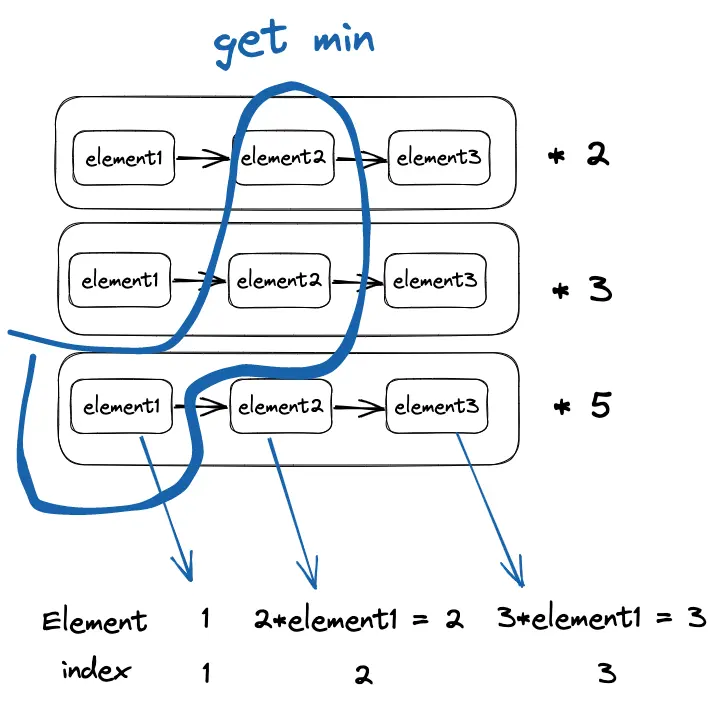
难点在于数学上的理解，代码上的操作其实就是多指针对多个list的element进行拼接(有说法称之为多路并归)。

图片可能画的还不够好，后面的*2 、 *3等指的是 element中的每一个元素在乘算之后的结果，构成了该行的新list，elementlist本身就是最终的list

元素1往往就是1，有些丑数题不将1作为元素，则最后求element的时候处理index

不断求min的过程中确定Element，而Element本身也作为上述list的元素来求新的值。

L378 有序矩阵中第 K 小的元素

给你一个 n x n 矩阵 matrix，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。 请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同的元素。

你必须找到一个内存复杂度优于 O(n2) 的解决方案。

例如 输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8 输出：13

---

其实也算是多路并归的一种思路，此题可以当做数组版本的 23. 合并K个升序链表 的变体。矩阵中的每一行都是排好序的，就好比多条有序链表，你用优先级队列施展合并多条有序链表的逻辑就能找到第 k 小的元素了。

L373 查找和最小的 K 对数字

给定两个以 升序排列 的整数数组 nums1 和 nums2, 以及一个整数 k。

定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2。

请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk)。

---

多路并归

nums是排好序的，对于示例的 nums1 = [1,7,11], nums2 = [2,4,6], k = 3，可以看做合并3个list，其分别是

[1, 2] -> [1, 4] -> [1, 6] [7, 2] -> [7, 4] -> [7, 6] [11, 2] -> [11, 4] -> [11, 6]

按照 23. 合并K个升序链表 的思路来合并，取出前 k 个作为答案即可。

合并数组

核心思路就是，不同于链表，数组是有明确边界的，所以在一些情况下，别忘了可以从尾部开始倒着进行一些操作

L88 合并两个有序数组

合并的题目，一种直接的思路是套用链表，两个指针指向两个数据源，然后比较后选出需要的创建新的数据源。

但是不同于链表只操作的是node之间的关联，在数组中，我们操作的直接就是数据本身。这道题目麻烦的是，要求直接合并到原来的数组1中，这意味着如果我们用链表的思路，那么我们会直接污染原始数据，即 nums1中的原始元素会被覆盖

而解法其实在本节最开始暗示了，就是backward双指针初始化在数组的尾部，然后从后向前进行合并，因为nums1中预留了空间，这样即便当覆盖了 nums1 中的元素时，这些元素也必然早就被用过了，不会影响答案的正确性。

L977 有序数组的平方

平方的特点是会把负数变成正数，所以一个负数和一个正数平方后的大小要根据绝对值来比较。

一种做法是先找到元素 0 (或最靠近0的元素)作为分界线，然后向左右扩展，执行合并有序数组的逻辑。

不过还有个更好的办法，不用找正负分界点，而是直接将双指针分别初始化在 nums 的开头和结尾，相当于合并两个从大到小排序的数组，和 88 题类似的backward的思路

L360 有序转化数组 (付费)

给你一个已经排好序的整数数组 nums 和整数 a, b, c。对于数组中的每一个元素 nums[i]，计算函数值 f(x) = ax2 + bx + c，请按升序返回结果数组。

输入：nums = [-4,-2,2,4], a = 1, b = 3, c = 5 输出：[3,9,15,33]

其实就是L977 有序数组的平方的加强版，977是本道题的a = 1, b = 0, c = 0 的特殊情况，所以这道题的关键也是在 nums 的开头和结尾设置 i, j 双指针相向而行，执行合并有序数组的逻辑，只不过这里需要考虑的情况更多了一些罢了。

即 a大于0是开头向下的二次函数，小于0是开头向上的。两者不同导致了我们双指针相向而行的之后，f(x)是不断变大还是变小的